
Your program should find the roots in all three situations (the lab 1 version should work when the discriminant = 0 or > 0) your modifications for lab 2 should handle the case when the discriminant is < 0. Runtime error, so the discriminant must be negated (i.e., multiplied by -1) before

Taking the square root of a negative number with the sqrt function causes a Simplify both top and bottom by the FOIL method. Since the i-terms are imaginary numbers, write out the actual value of and.

Sqrt(descriminant)/2a with an ‘i’ character printed at the endĭ. Explanation: Multiply the top and the bottom by the conjugate of the denominator. The imaginary part (3i in the example) is calculated by the formula The real part (6 in the example) is calculated by the formula -b/2aĬ. Complex numbers are displayed with a real part and an imaginary part: e.g., 6 +ī. The discriminant, b^2 - 4ac, describes the roots of a quadratic equation: if it is greater than or equal to 0, there are two real roots and if it is less than 0, there are two complex roots.Ī. If the user enters a 0 for a, print an appropriate error message and end the program (skip all calculations, do not loop). The quadratic formula fails if coefficient ais 0. I got it to work with the complex include but I don't think that's what is wanted. This is why not the complex include these were the instruction I was given but doesn't quite make sense to me. Rootvalue2 = (-b - sqrt(b * b - 4 * a * c)) / (2 * a) Ĭout <<"The first Root Value = " << rootvalue1 << endl //Roo AnswerĬout <<"The second Root Value = " << rootvalue2 << endl Rootvalue1 = (-b + sqrt(b * b - 4 * a * c)) / (2 * a) // Quadratic formula If (a = 0) //If user enters 0 it will quit the program and give them error message. Thanks!Įdit: Also is there a way to do this without the #include \ #include
#Imaginary numbers help code
What can I add or adjust in my code to help get the program to show imaginary 'complex numbers'. On the real axis, the real part of a complex number a + bi is plotted.ĭe Moivre’s theorem generalizes the relation to show that to raise a complex number to the n th power, the absolute value is raised to the n th power and the argument is multiplied by n.Hey guys I'm new to programing and I made a program to solve quadratic formula but it doesn't work with imaginary numbers when the number is negative I get something like this -1.#IND.
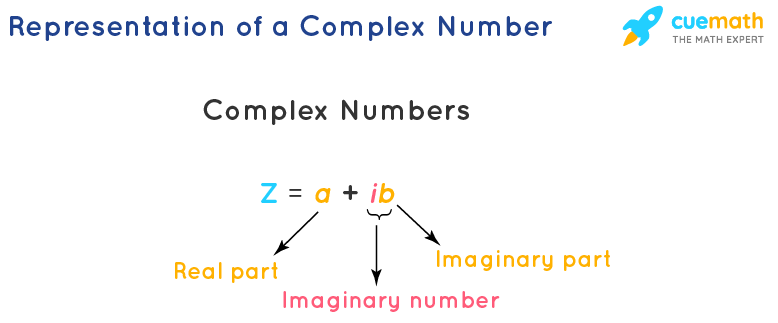
Polar Form Of A Complex Number – Let, z be the complex number a + bi,.Modulus – In the complex plane, the modulus is the distance between the plot of a complex number and the origin.Imaginary Axis – The axis in the complex plane that in usual practice coincides with the y-axis of the rectangular coordinate system, and on which the imaginary part bi of the complex number a + bi is plotted.Complex Plane – It is a plane which has two perpendicular axis, on which a complex number a + bi is plotted having the coordinate as (a, b).Complex Conjugate – For a given complex number a + bi, a complex conjugate is a – bi.Argument – Argument is the angle we create by the positive real axis and the segment connecting the origin to the plot of a complex number in the complex plane.Source:en. Terms used in Complex Numbers: Division of Complex Numbers: \(\frac\).Multiplication Conjugates: (a+bi) × (a+bi) = a 2+b 2.Multiplication of Complex Numbers: (a+bi)×(c+di) = (ac−bd) + (ad+bc)i.Subtraction of Complex Numbers: (a+bi)−(c+di) = (a−c) + (b−d)i.Addition of Complex Numbers: (a+bi)+(c+di) = (a+c) + (b+d)i.Here, real part is equal with each other and imaginary parts are equal i.e. In complex number, a is the real part and b is the imaginary part of the complex number. What is a Complex Number?Ī complex number is a number having both real and imaginary parts that can be expressed in the form of a + bi, where a and b are real numbers and i is the imaginary part, which should satisfy the equation i 2 = −1. Let us learn complex number formula here. The concept of the two-dimensional complex plane is explained in detail with the help of a complex number by using the horizontal axis for the real part and the vertical axis for the imaginary part.

A combination of a real number and an imaginary number forms a complex number.


 0 kommentar(er)
0 kommentar(er)
